Factor Analysis and Multidimensional Analysis

Alex Reinhart
areinhar@stat.cmu.edu

Statistics & Data Science 36-468/668

David Brown
dwb2@andrew.cmu.edu

Dept. of English

Fall 2025

Linguistic correlation

Correlation

  • Many linguistic variables are related to each other in some way
  • That is, if we count their occurrence in texts, the rate of occurrence will be correlated
  • If one occurs more often, the other is likely to occur more (or less) often

Correlation in language

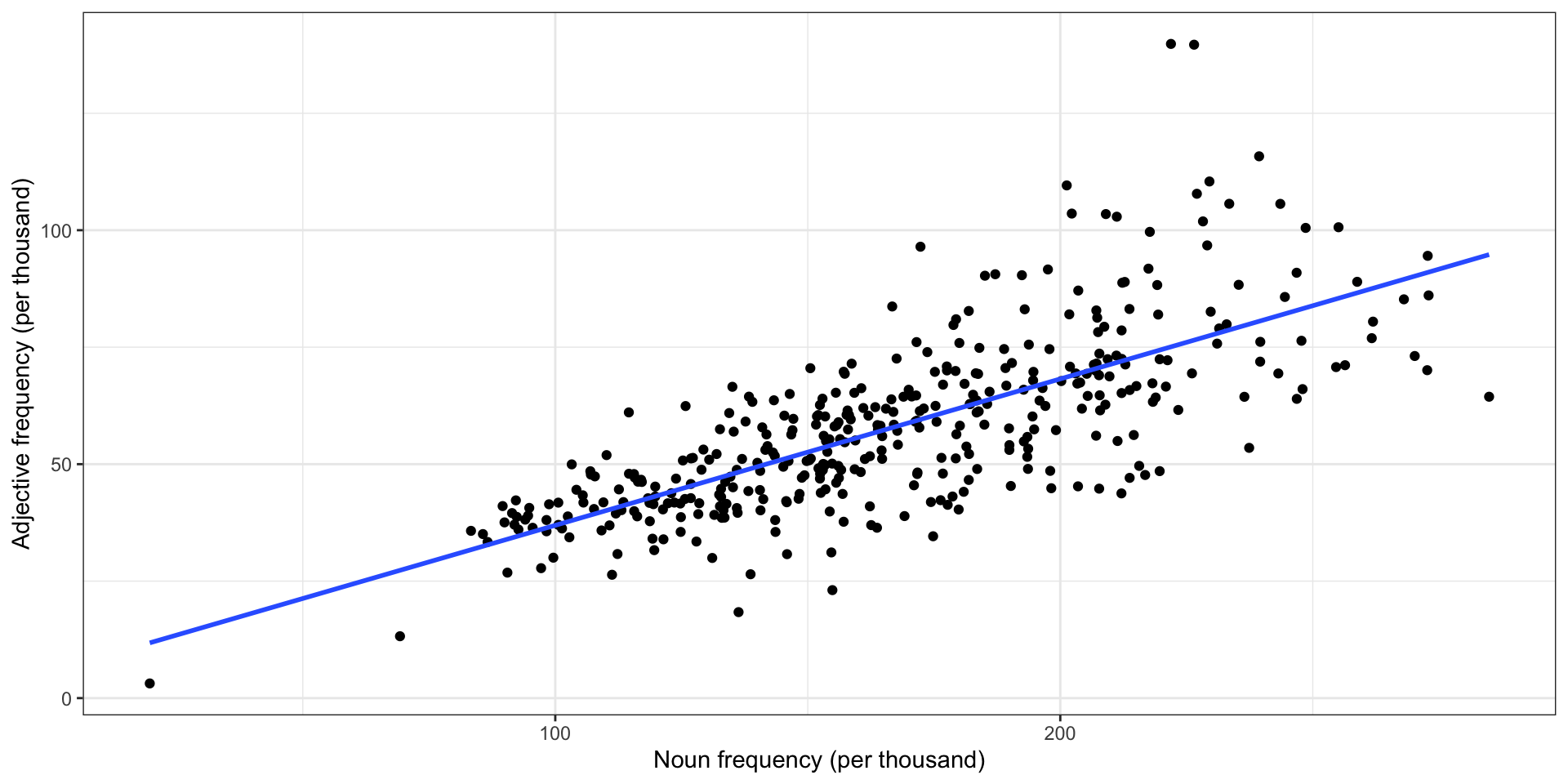
  • In English, the relative frequency of adjectives is correlated to the relative frequency of nouns
  • Adjectives modify nouns, so they come together

Get Out is an extraordinary movie, a great catapulting leap forward…

  • This isn’t universal—see Hemingway’s novels—but it is a strong correlation

Adjectives vs. nouns in COCA

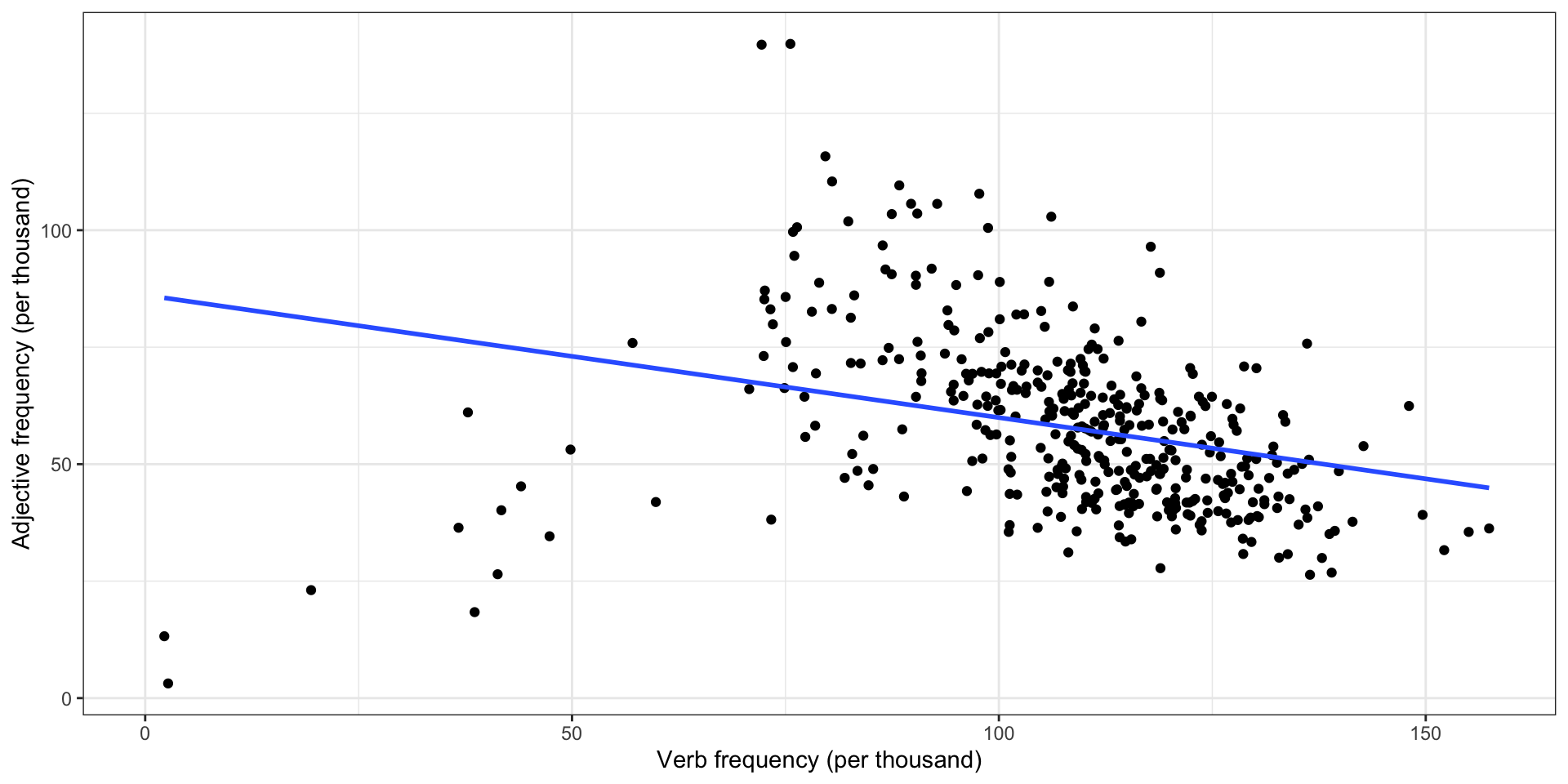
Adjectives vs. verbs in COCA

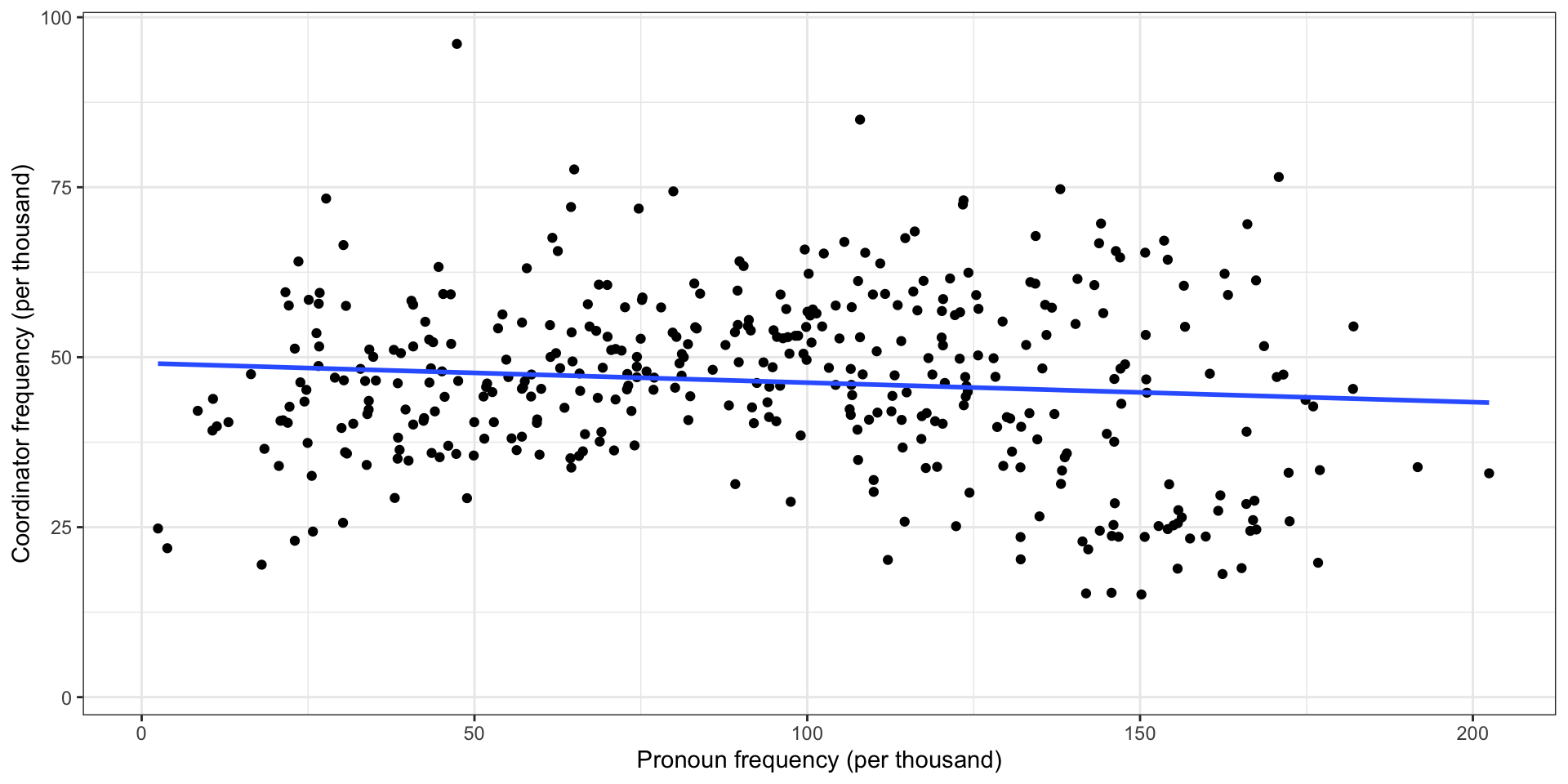
Pronouns vs. coordinators in COCA

Correlation measures

Pearson correlation

  • Pearson correlation is the correlation coefficient you probably know best
  • The correlation \(\rho\) is in \([-1, 1]\); 0 means no linear correlation, 1 means perfect linear correlation

\[ \rho(X, Y) = \frac{\operatorname{cov}(X, Y)}{\sigma_X \sigma_Y} = \frac{\sum_{i=1}^n (x_i - \bar x) (y_i - \bar y)}{\sqrt{\sum_{i=1}^n (x_i - \bar x)^2} \sqrt{\sum_{i=1}^n (y_i - \bar y)^2}} \]

For example,

cor(noun_adj$NOUN, noun_adj$ADJ, use = "complete.obs")
[1] 0.6740684

Spearman correlation

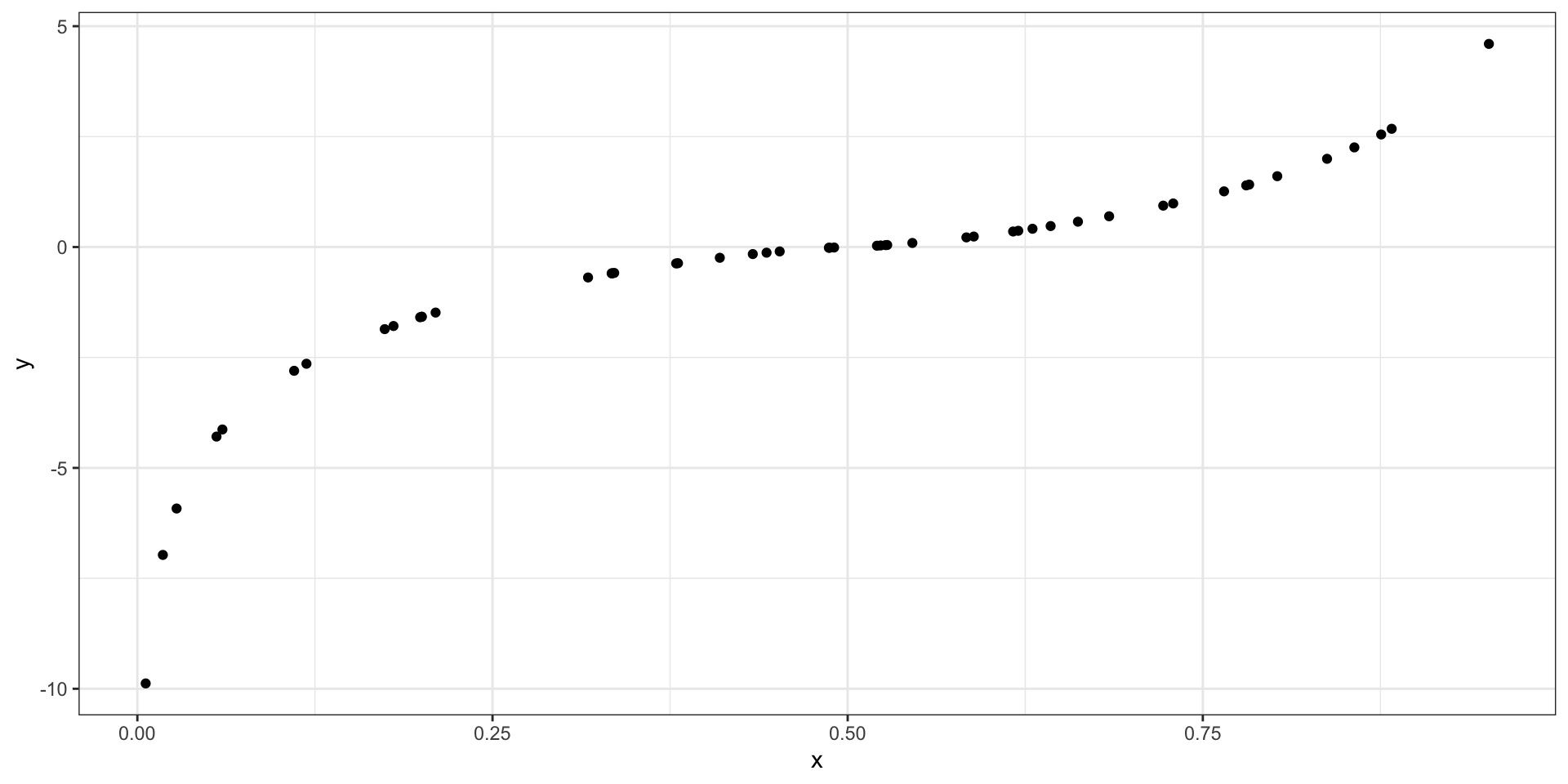
  • Linear (Pearson) correlation only measures linear relationships; a strong but curved relationship has correlation \(|\rho| < 1\)
  • Spearman correlation uses the ranks, so it measures any monotone relationship
Document Adjectives Adj. rank Nouns Noun rank
news_35 3.1 1 19.7 1
news_02 13.2 2 69.3 3
acad_48 18.4 3 136.3 107
news_26 23.1 4 154.9 168
tvm_10 26.4 5 111.2 41
news_44 26.5 6 138.7 112
tvm_42 26.8 7 90.5 9
tvm_16 27.8 8 97.2 19
spok_14 30.0 9 131.1 86
tvm_40 30.0 10 99.6 23

Correlation examples

cor(x, y)
[1] 0.8839384
cor(x, y, method = "spearman")
[1] 1

Cut-offs

Rough cut-off values are used to indicate the size of correlation (Cohen 1988: 79-80); this is a measure of effect size:

  • 0 no effect
  • ± 0.1 small effect
  • ± 0.3 moderate effect
  • ± 0.5 strong effect

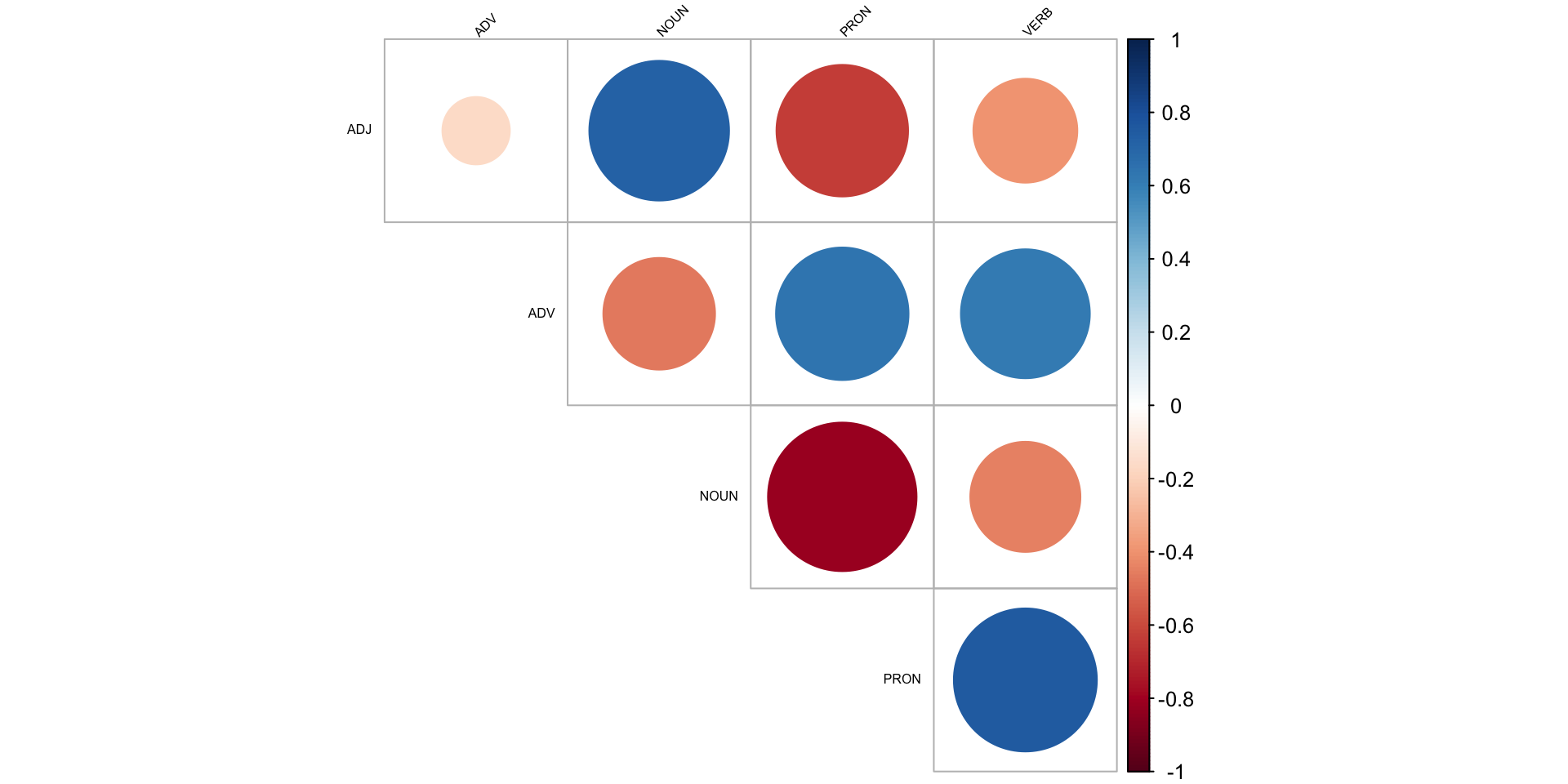
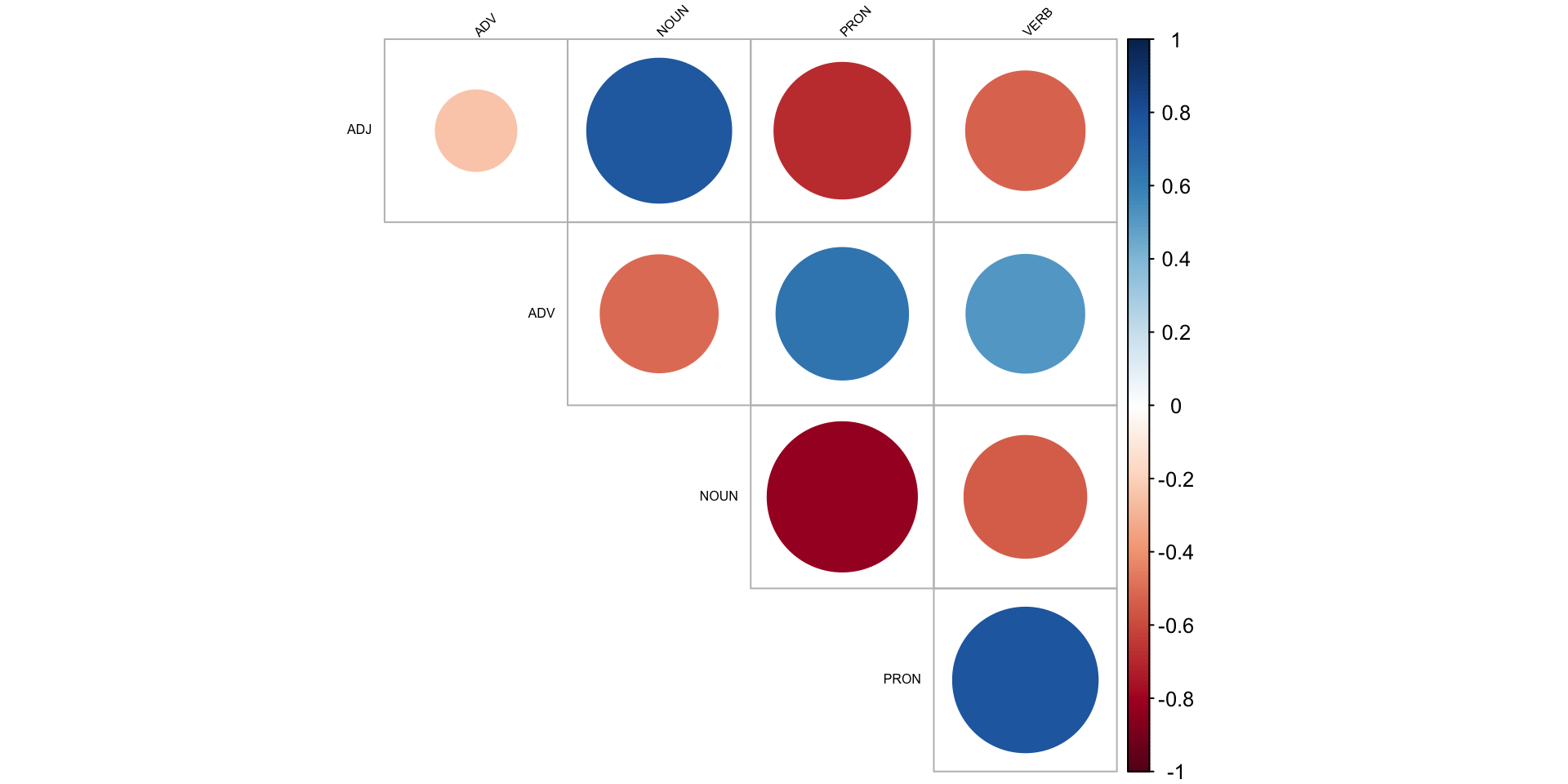
Correlation matrices

Every pairwise correlation between a set of variables can be presented in a matrix:

Pearson correlation

ADJ ADV NOUN PRON VERB
ADJ 1.00 −0.17 0.72 −0.64 −0.40
ADV −0.17 1.00 −0.46 0.65 0.61
NOUN 0.72 −0.46 1.00 −0.81 −0.45
PRON −0.64 0.65 −0.81 1.00 0.75
VERB −0.40 0.61 −0.45 0.75 1.00

Spearman correlation

ADJ ADV NOUN PRON VERB
ADJ 1.00 −0.24 0.77 −0.68 −0.52
ADV −0.24 1.00 −0.51 0.64 0.51
NOUN 0.77 −0.51 1.00 −0.82 −0.55
PRON −0.68 0.64 −0.82 1.00 0.77
VERB −0.52 0.51 −0.55 0.77 1.00

The matrix

  • has 1 on the diagonal
  • is symmetric
  • can be turned into a cool heatmap

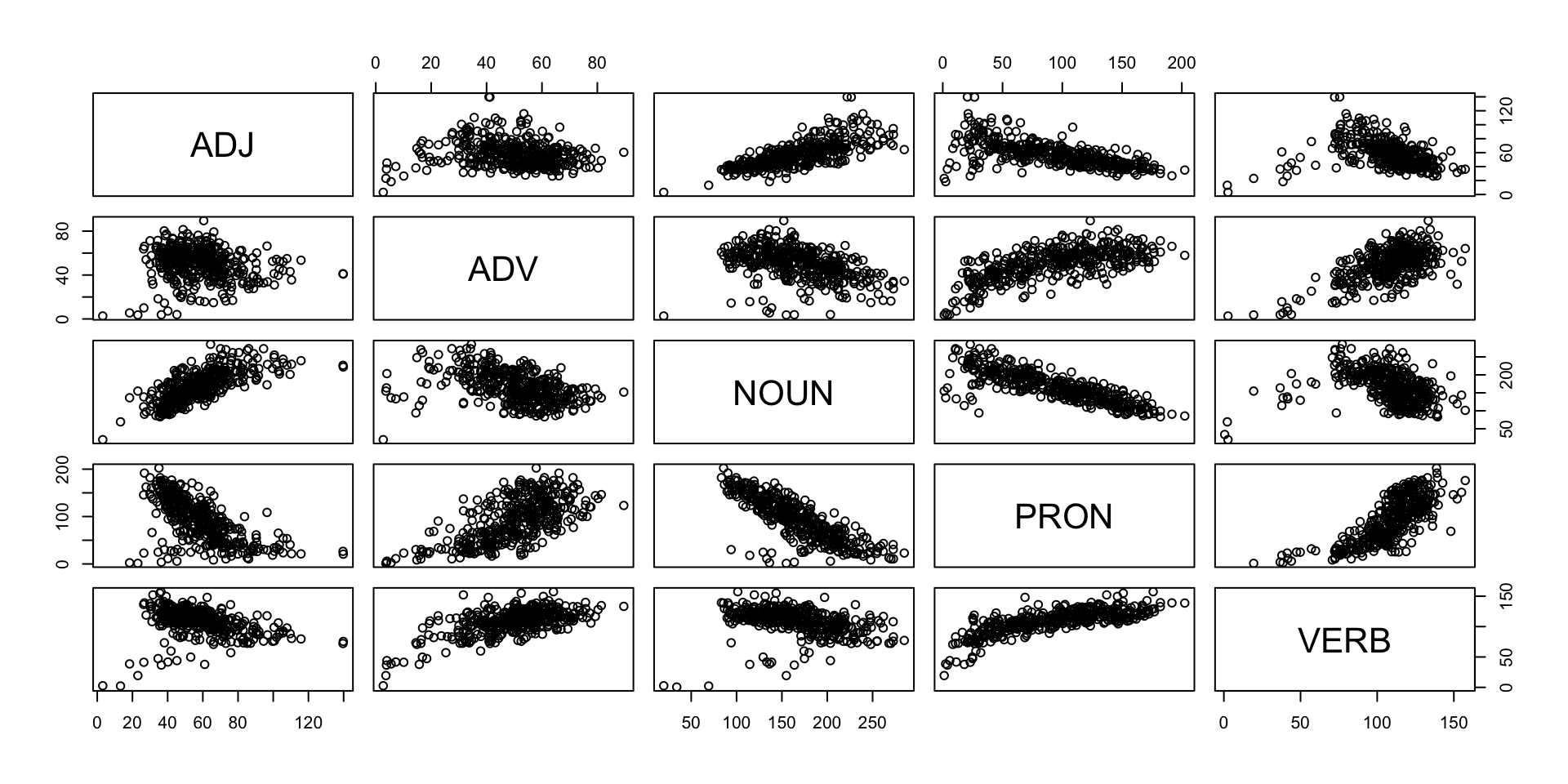
Correlation plots

Pair plots

pairs(counts)

Coefficient of determination

  • Pearson’s correlation coefficient r can be used to account for the amount of variance in one variable “explained” by the other variable
  • For this, calculate its square: \(R^2\)

Reporting your results

There is a strong positive correlation (\(r = .55\), 95% CI [.48, .61]) between the number of nouns and the number of adjectives used in American English. This value, however, is not as large as the correlation between verbs and pronouns (\(r = .75\), 95% CI [.71, .78]), each of which explains more than half the variance of the other (\(R^2 = 56\)%).

There is a strong negative correlation (\(r_s = -.84\), \(p < .01\)) between the number of nouns and the number of pronouns used in American English. These show a complementary distribution.

Reporting your results

American English verbs and adjectives are in an inverse proportional relationship (\(r = -.61\)**), as are verbs and nouns (\(r = -.67\)**). The negative correlation between verbs and coordinators is near zero, however (\(r = -.04\)), indicating those lexical classes have no observable relationship.

(Stargazing!)

Factor analysis

Basic motivation

  • Let \(X\) be an \(n \times p\) matrix of observed data, such as rates of \(p\) parts of speech in \(n\) documents
  • If columns 1, 2, and 4 are strongly correlated with each other, and 3, 5, and 6 are also strongly correlated with each other, but there’s little correlation between the groups, then:
    • Maybe 1, 2, and 4 measure one underlying “factor”
    • Maybe 3, 5, and 6 measure a different factor
    • These two factors might “explain” most of the variation in \(X\)
  • How do we automatically find the factors?

More mathematically

  • Let \(X\) be an \(n \times p\) matrix of observed data, such as rates of \(p\) parts of speech in \(n\) documents
  • Suppose there are \(m\) common factors, where \(m < p\)
  • Suppose each document \(i\) can be expressed with its common factors, plus some noise

What should this remind you of?

The factor model

The factor model is that \[ \underbrace{X}_{n \times p} = \underbrace{F}_{n \times m} \underbrace{L}_{m \times p} + \underbrace{\epsilon}_{n \times p} \] where \(X\) has been centered so its columns have mean 0.

  • \(F\): each document’s factor coordinates
  • \(L\): loading of each factor on original variables
  • \(\epsilon\): mean 0, diagonal variance noise
  • \(F\) and \(\epsilon\) are independent

Examples

\[ X = FL + \epsilon \]

  • \(n\) students solve \(p\) calculus test questions
    • Most variation in scores can be explained by \(m = 1\) factor: how good you are at calculus
  • \(n\) people take \(p\) personality test questions
    • Most personality features can be explained in terms of \(m = 5\) factors (the Big Five personality traits)
  • \(n\) documents have \(p\) different linguistic features measured
    • The features represent \(m\) underlying factors, like formality, information density, etc.

Fitting a factor analysis

  • Factor analysis should remind you of PCA
    • But PCA doesn’t have \(\epsilon\), so factor analysis does not explain independent noise, only variance that is shared
  • We can find \(F\) and \(L\) by starting with PCA
  • Alternately, assume \(\epsilon\) and \(F\) are both multivariate normal
    • Then do maximum likelihood estimation
  • Unlike PCA, we do not require factors to be orthogonal
  • Any rotation of the factors is equivalent, so we choose based on interpretability

Multidimensional Analysis (MDA)

Biber’s MDA

  • Multidimensional analysis (MDA) was developed by Biber (1985)
  • Goal is to use factor analysis to systematically identify principles of language variation (Biber 1988)

Stages of MDA

  1. Identify of relevant variables
  2. Extract factors from variables
  3. Interpret factors as functional dimensions
  4. Place document categories on the dimensions

Step 1: Identify relevant variables

Biber defined 67 linguistic features, like

  • past tense verbs
  • present tense verbs
  • first-person pronouns
  • second-person pronouns
  • that relative clauses
  • present participles
  • pied piping
  • mean word length
  • downtoners
  • predictive models
  • possibility modals
  • contractions

These features distinguish different types of written and spoken English.

Step 2: Extract factors from variables

  • From the many relevant variables, extract a few factors
  • We can just use factor analysis: \[ X = FL + \epsilon \]
    • \(X\): matrix of features for each document, centered & scaled
    • \(F\): each document’s factor coordinates
    • \(L\): loading of each factor on original features
  • To ensure there are only a few factors and each is interpretable,
    • Only include variables that are correlated with at least some other variables (e.g., \(|\rho| \geq 0.2\))
    • For factors, only keep loadings that are a minimum size

Step 2: Loading the corpus

library(cmu.textstat)
library(tidyverse)
library(quanteda)
library(nFactors)
library(mda.biber)

brown_biber <- brown_biber |>
  left_join(dplyr::select(brown_meta, doc_id, text_type)) |>
  mutate(text_type = as.factor(text_type)) |>
  column_to_rownames("doc_id") |>
  relocate(text_type)

Step 2: Variables are highly correlated

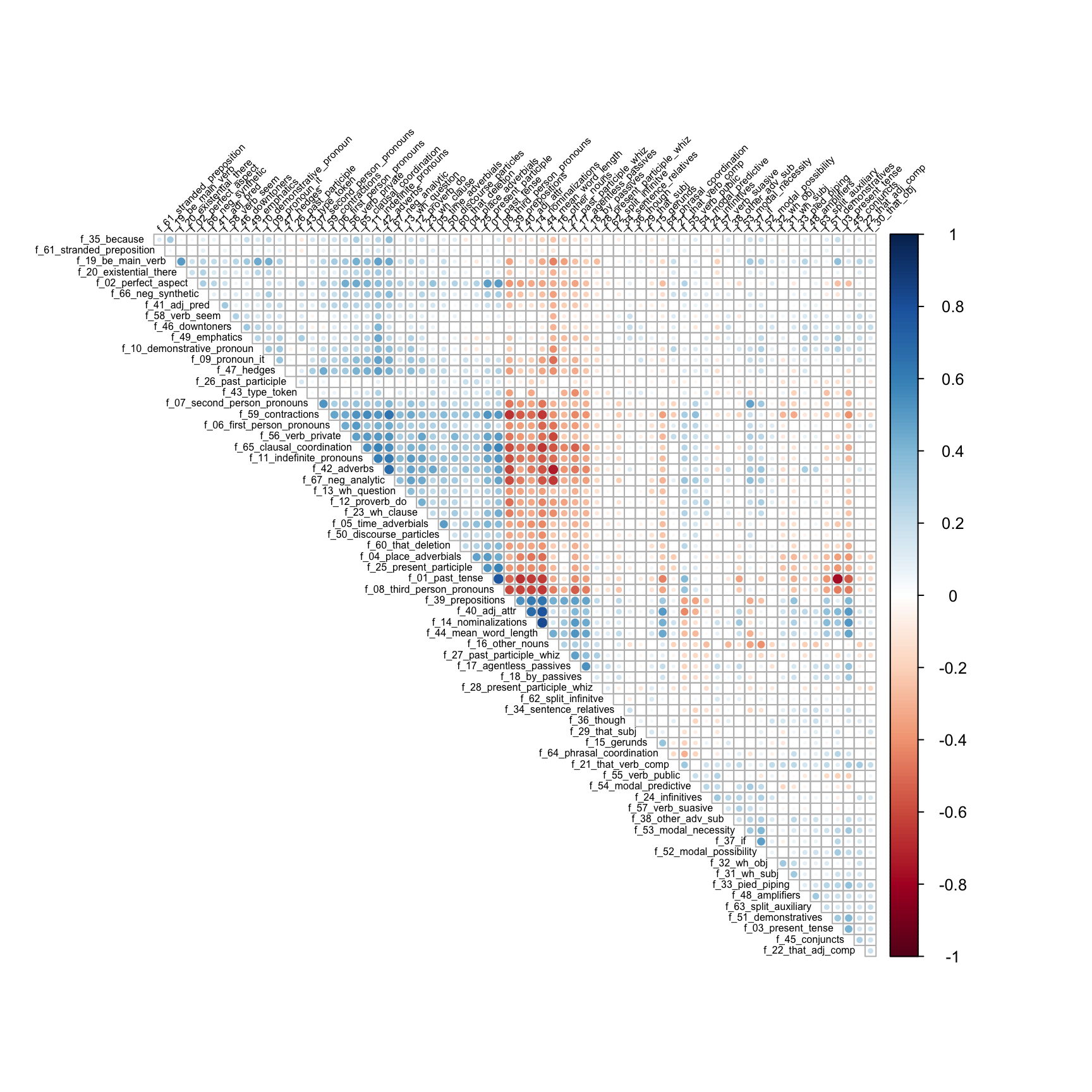
Step 2: Determine the number of factors

screeplot_mda(brown_biber)

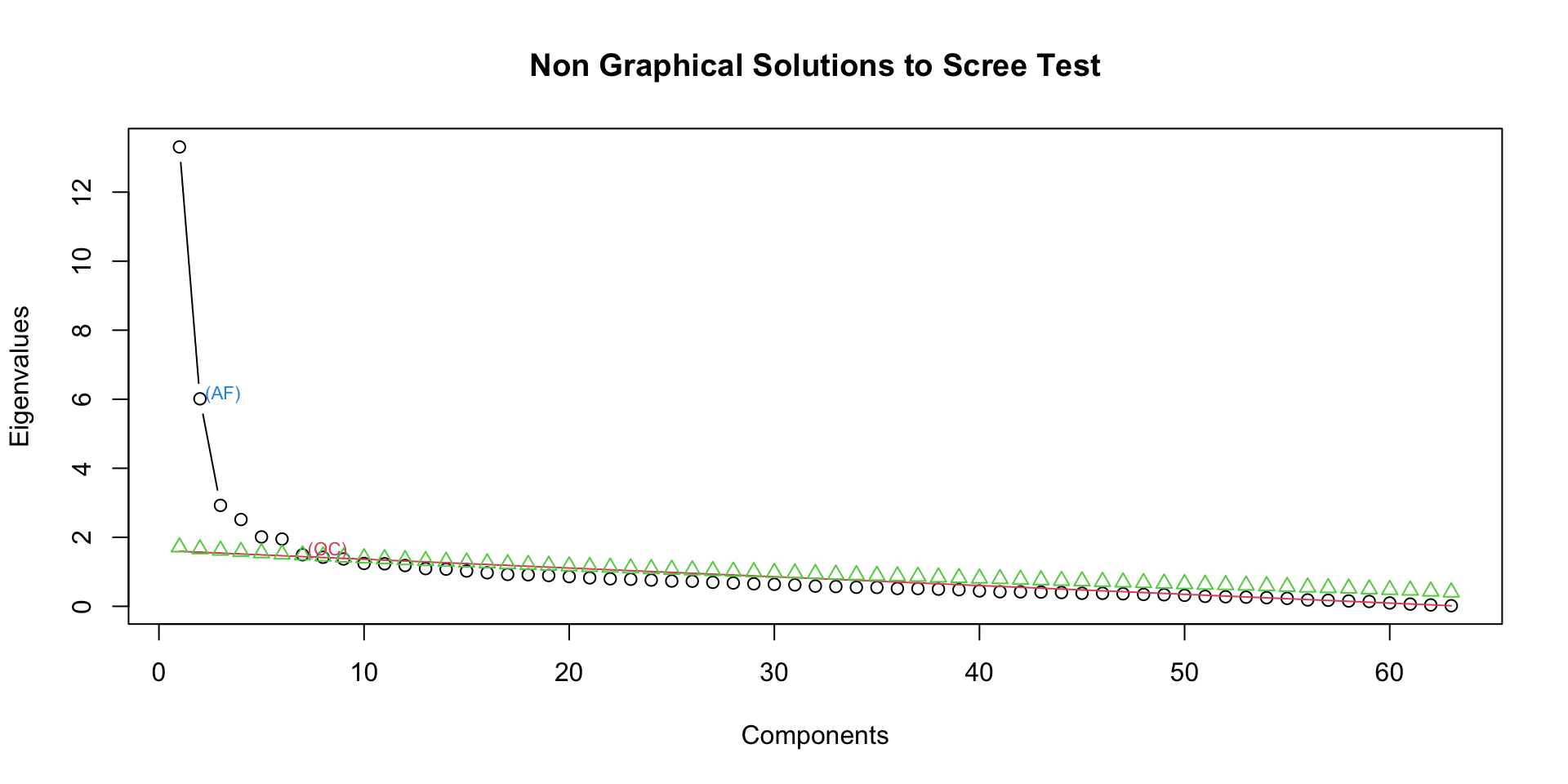
Step 2: Rotate the factors

  • If we have \(m\) factors, they span an \(m\)-dimensional space
  • Any other basis for that space can yield an identical fit!
  • So choose the factors that help us interpret each factor as a distinct thing

For example, suppose we have \(p = 6\) variables and choose \(m = 2\)

Step 2: Rotate the factors

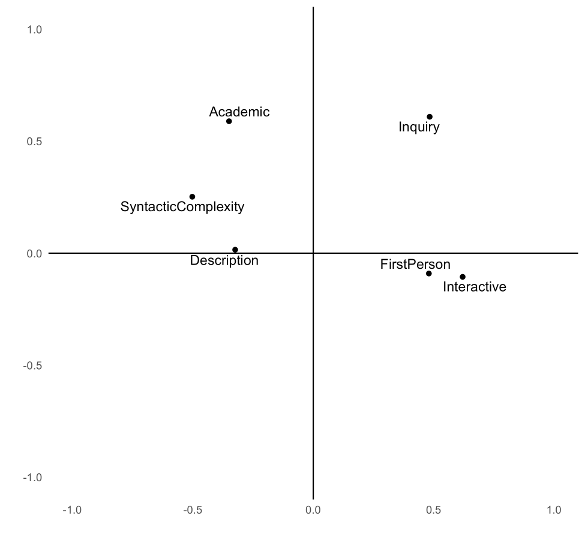
Step 2: Varimax rotation

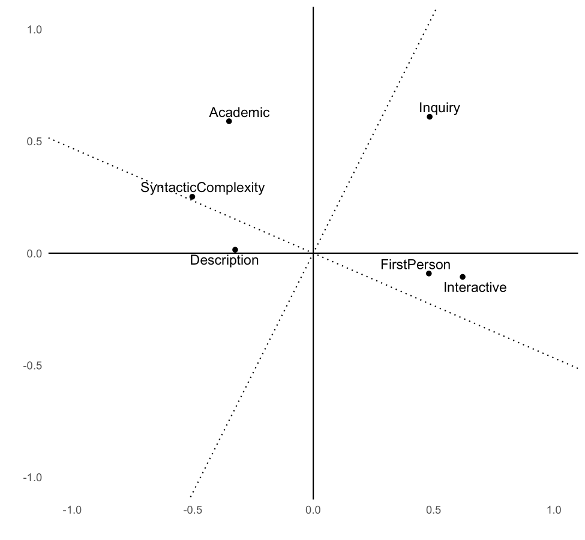
Step 2: Promax rotation

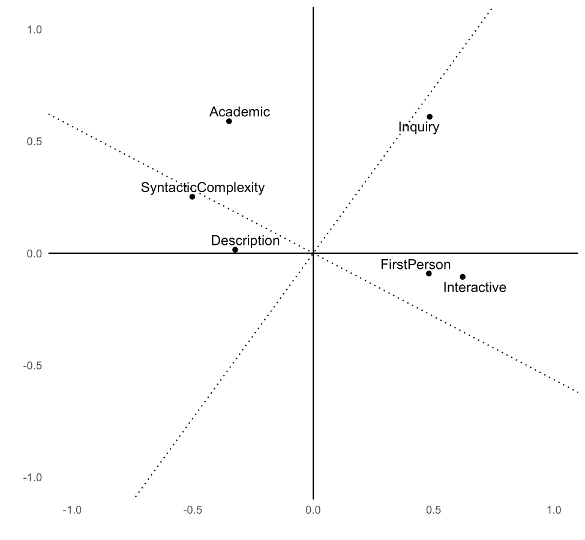
Step 3: Interpret the rotated factors

Feature Factor1 Factor2 Factor3
f_39_prepositions −0.68 −0.23 −0.06
f_07_second_person_pronouns 0.66 −0.11 −0.14
f_44_mean_word_length −0.65 −0.36 0.04
f_59_contractions 0.61 0.25 −0.03
f_03_present_tense 0.60 −1.06 −0.04
f_67_neg_analytic 0.57 0.20 0.38
f_42_adverbs 0.57 0.21 0.51
f_12_proverb_do 0.54 0.04 0.14
f_37_if 0.53 −0.27 0.12
f_27_past_participle_whiz −0.53 0.08 −0.11

Step 4: Place documents on the factor dimensions

\[ X = FL + \epsilon \]

  1. Threshold the factor loadings \(L\) to pick the large loadings
  2. For each dimension,
    • Sum up the variables with large positive loadings
    • Subtract those with large negative loadings
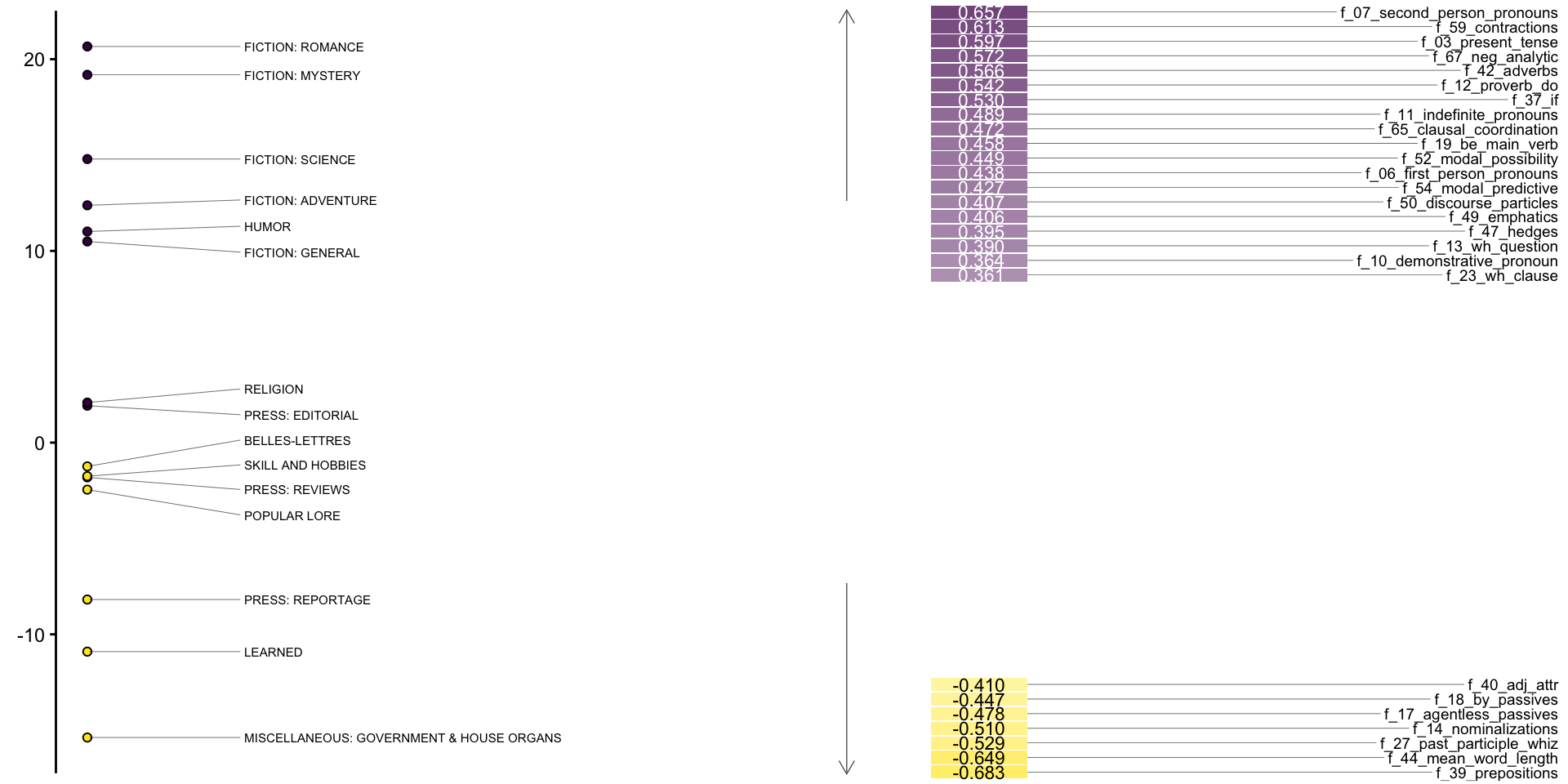
  3. Calculate for each document and take means per category/corpus/text type

Step 4: Placement on factor 1

Step 4: Placement on all factors

library(gtsummary)

f1 <- lm(Factor1 ~ group, data = bc_mda)
f2 <- lm(Factor2 ~ group, data = bc_mda)
f3 <- lm(Factor3 ~ group, data = bc_mda)

tbl_merge(list(
  tbl_regression(f1, intercept = TRUE),
  tbl_regression(f2, intercept = TRUE),
  tbl_regression(f3, intercept = TRUE)
  ),
  tab_spanner = c("Factor 1", "Factor 2", "Factor 3")
)

Step 4: Placement on all factors

Characteristic
Factor 1
Factor 2
Factor 3
Beta 95% CI p-value Beta 95% CI p-value Beta 95% CI p-value
(Intercept) -1.2 -3.7, 1.2 0.3 -0.81 -2.1, 0.51 0.2 1.7 0.20, 3.3 0.027
group








    BELLES-LETTRES — —
— —
— —
    FICTION: ADVENTURE 14 9.0, 18 <0.001 15 12, 17 <0.001 -0.81 -3.7, 2.1 0.6
    FICTION: GENERAL 12 7.1, 16 <0.001 13 11, 16 <0.001 -0.23 -3.1, 2.7 0.9
    FICTION: MYSTERY 20 15, 25 <0.001 14 12, 17 <0.001 3.1 -0.02, 6.2 0.051
    FICTION: ROMANCE 22 17, 27 <0.001 14 12, 17 <0.001 2.9 0.02, 5.8 0.048
    FICTION: SCIENCE 16 7.1, 25 <0.001 8.1 3.3, 13 0.001 5.4 -0.21, 11 0.059
    HUMOR 12 4.8, 20 0.001 7.3 3.2, 11 <0.001 2.9 -1.7, 7.6 0.2
    LEARNED -9.7 -13, -6.3 <0.001 -7.8 -9.6, -5.9 <0.001 -0.11 -2.2, 2.0 >0.9
    MISCELLANEOUS: GOVERNMENT & HOUSE ORGANS -14 -19, -9.6 <0.001 -9.6 -12, -7.1 <0.001 -9.2 -12, -6.3 <0.001
    POPULAR LORE -1.2 -5.1, 2.7 0.5 -0.58 -2.7, 1.5 0.6 -2.4 -4.8, 0.09 0.059
    PRESS: EDITORIAL 3.2 -1.6, 7.9 0.2 -2.3 -4.8, 0.28 0.081 -0.87 -3.8, 2.1 0.6
    PRESS: REPORTAGE -6.9 -11, -2.9 <0.001 0.71 -1.5, 2.9 0.5 -10 -13, -7.8 <0.001
    PRESS: REVIEWS -0.57 -6.2, 5.1 0.8 -2.9 -6.0, 0.18 0.065 -3.9 -7.4, -0.29 0.034
    RELIGION 3.3 -2.3, 9.0 0.2 -3.8 -6.9, -0.75 0.015 4.3 0.73, 7.9 0.018
    SKILL AND HOBBIES -0.51 -4.8, 3.8 0.8 -5.6 -7.9, -3.2 <0.001 -5.1 -7.8, -2.4 <0.001
Abbreviation: CI = Confidence Interval

Common linguistic variables

Biber features

  • Developed by Biber (1988) for studying different registers of English
  • 67 features, mostly counts/rates, based on pattern-matching features in text
  • Good for distinguishing formal/informal texts, informational vs. interactive, etc.
  • Can be automatically tagged with pseudobibeR: https://cran.r-project.org/package=pseudobibeR

DocuScope

  • Developed at CMU over 25 years
  • Based on a dictionary of millions of phrases grouped into rhetorical categories
  • Examples:
    • Description
    • Academic
    • Information
    • Interactivity
    • Positive
    • Negative
  • Can be automatically tagged with a spaCy model trained on the dictionary: https://docuscospacy.readthedocs.io/en/latest/docuscope.html

Works cited

Biber, Douglas. 1985. “Investigating Macroscopic Textual Variation Through Multifeature/Multidimensional Analyses.” Linguistics 23 (2): 337–60. https://doi.org/10.1515/ling.1985.23.2.337.
———. 1988. Variation Across Speech and Writing. Cambridge University Press.