Cluster Analysis

Alex Reinhart
areinhar@stat.cmu.edu

Statistics & Data Science 36-468/668

David Brown
dwb2@andrew.cmu.edu

Dept. of English

Fall 2025

Two types of cluster analysis

  • Hierarchical agglomerative clustering
  • \(K\)-means clustering

Hierarchical clustering

Hierarchical clustering

Standardize the data

\[ z = \frac{\text{value} - \text{mean}}{\text{standard deviation}} \]

Standardized data

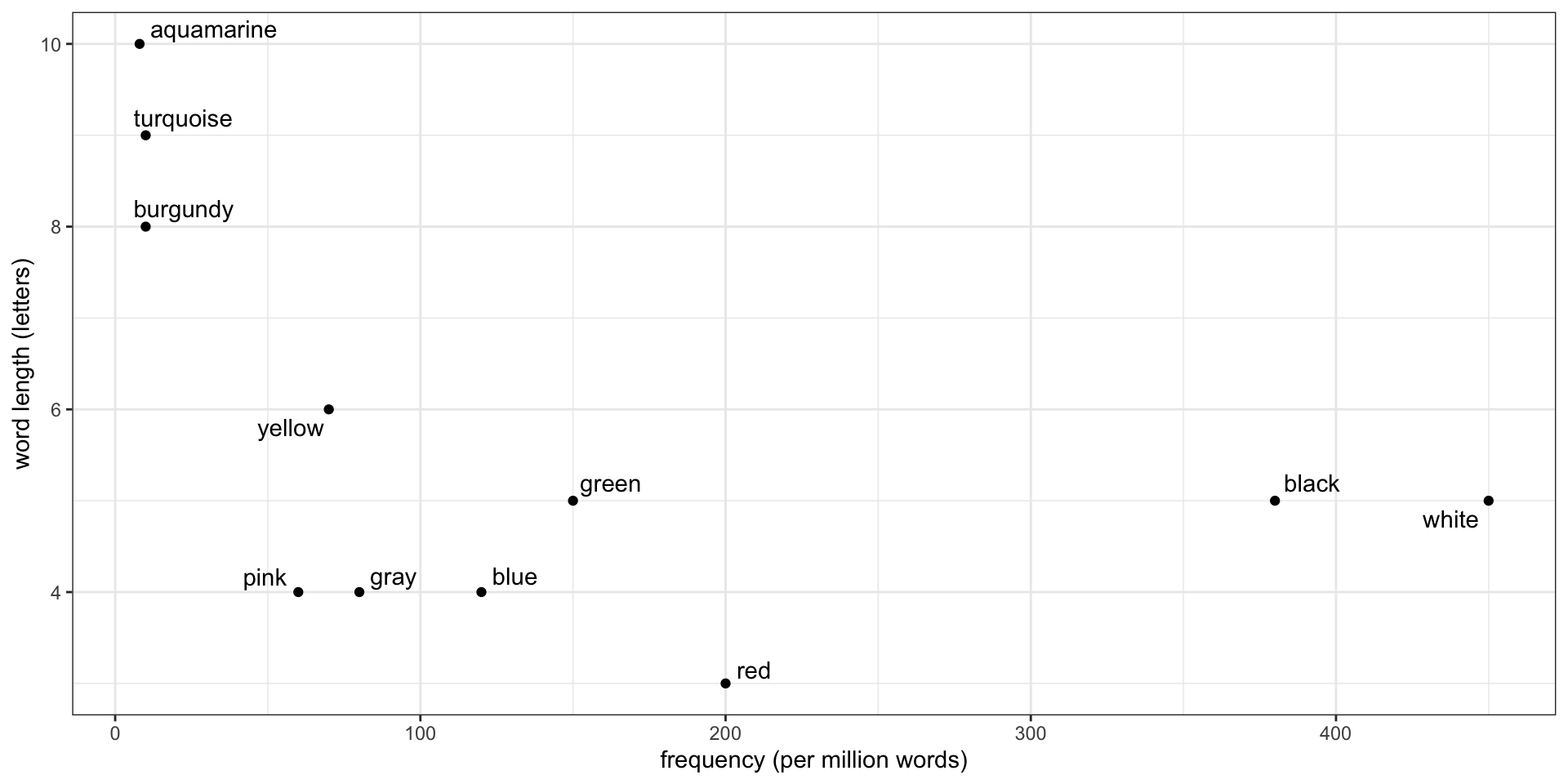
Clustering requires distances

  • To cluster, group nearby points
  • What does “nearby” mean? Options:
  1. Euclidean distance: \[\begin{align*} \operatorname{dist}(a, b) &= \sqrt{(a_x - b_x)^2 + (a_y - b_y)^2} \\ &= \|a - b\|_2 \end{align*}\]
  2. Manhattan distance: \[\begin{align*} \operatorname{dist}(a, b) &= |a_x - b_x| + |a_y - b_y| \\ &= \|a - b\|_1 \end{align*}\]

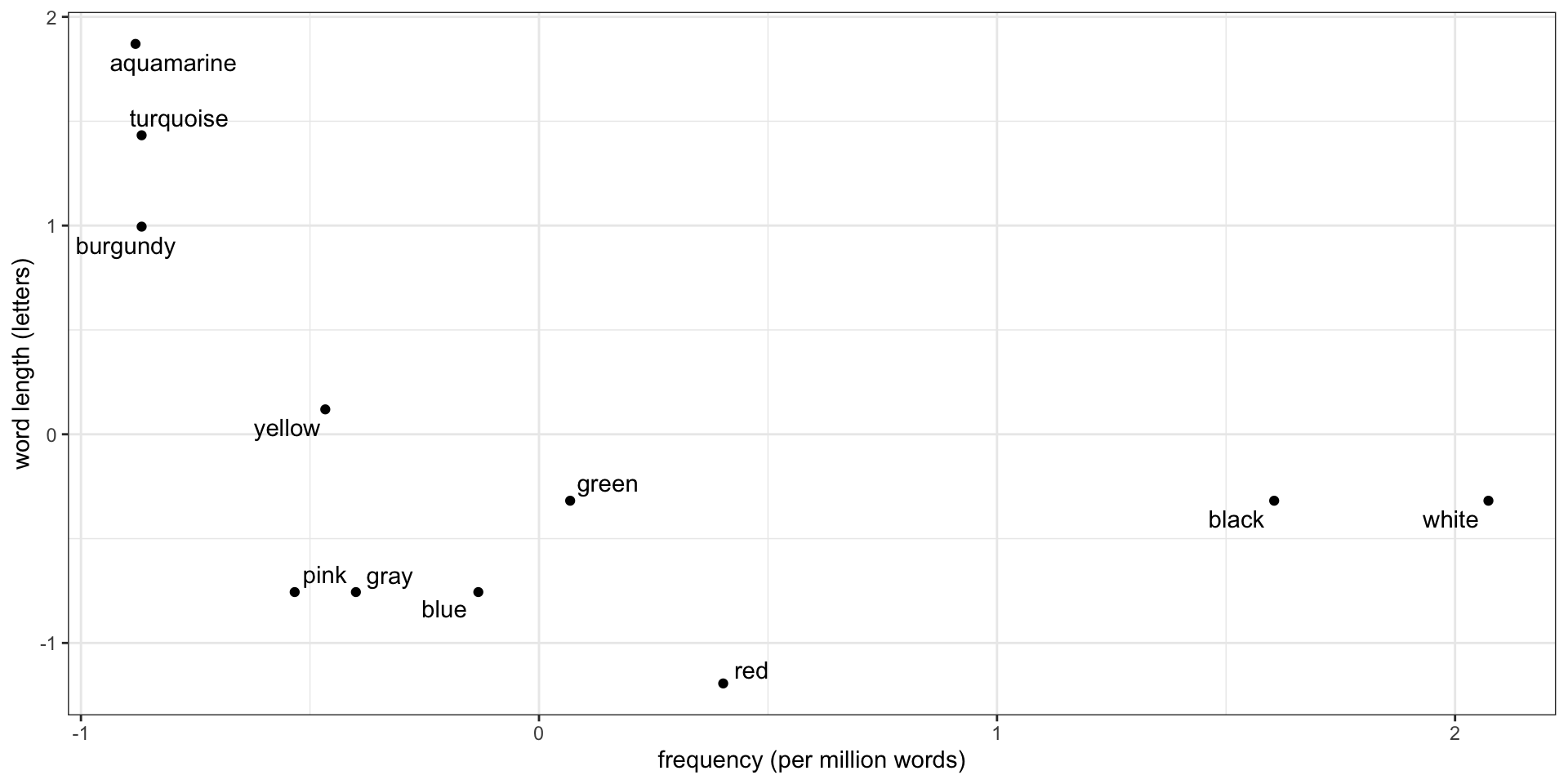
Find the closest pair of points

Euclidean \(\operatorname{dist}(\text{pink}, \text{gray}) = 0.13\)

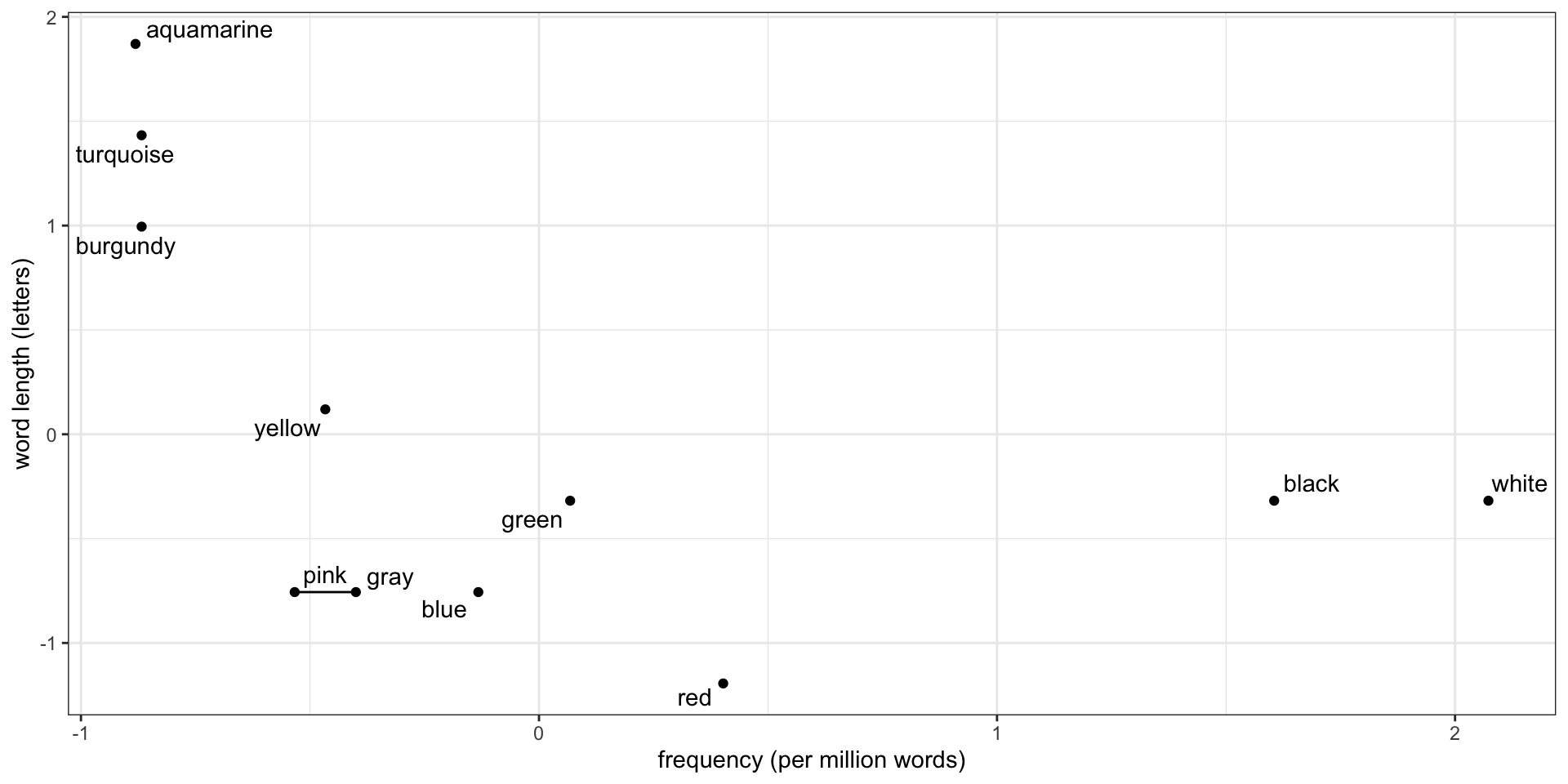
Then find the next closest

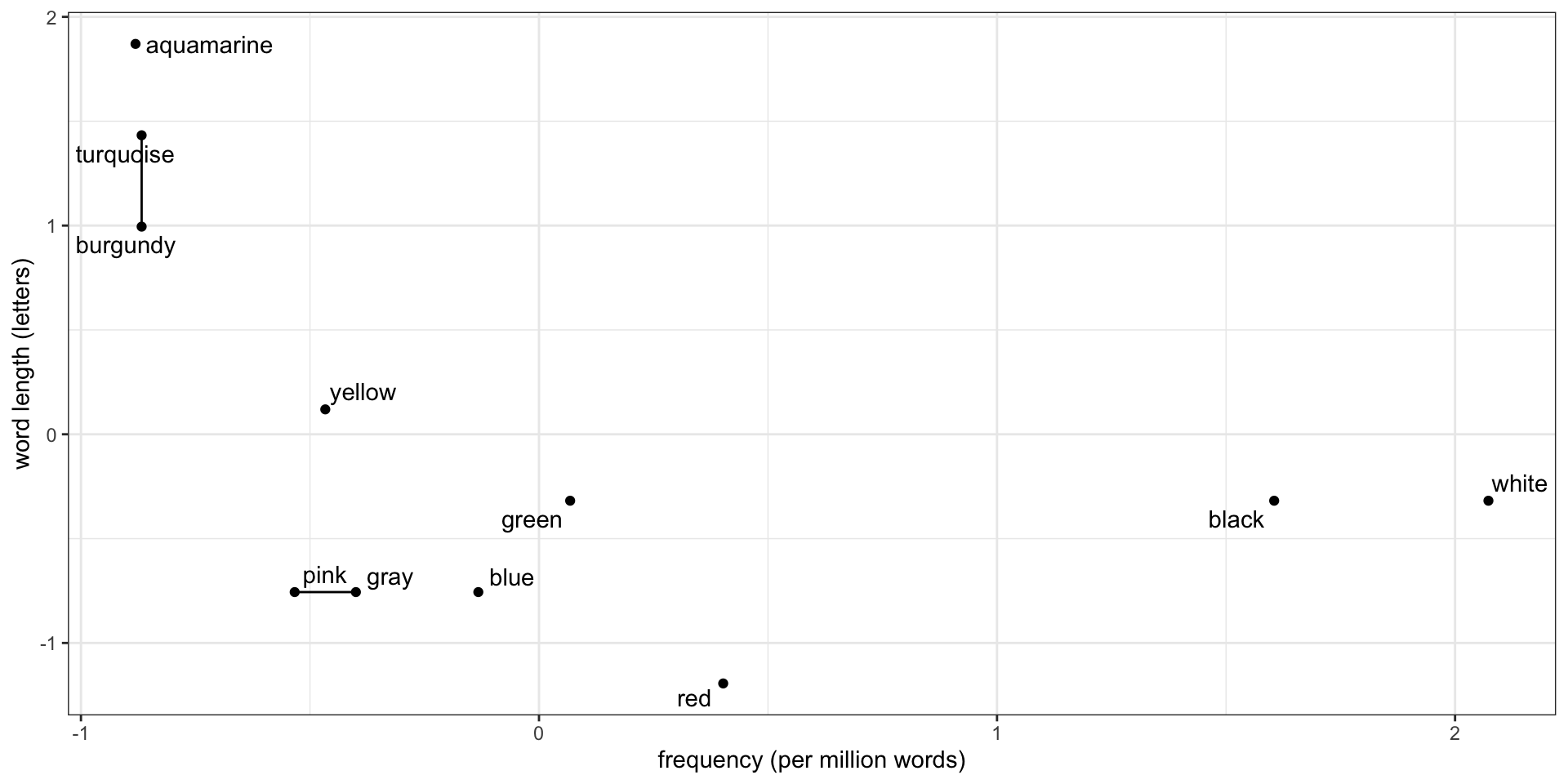
But how close is a point to a cluster?

How close is blue to the pink-gray cluster? How we measure this is called the linkage:

  • Distance from blue to the nearest point in the cluster: single linkage
  • Distance from blue to the farthest point in the cluster: complete linkage
  • Average distance from blue to each point in the cluster: average linkage
  • Change in squared distances within the clusters: Ward’s method

Single linkage dendrogram

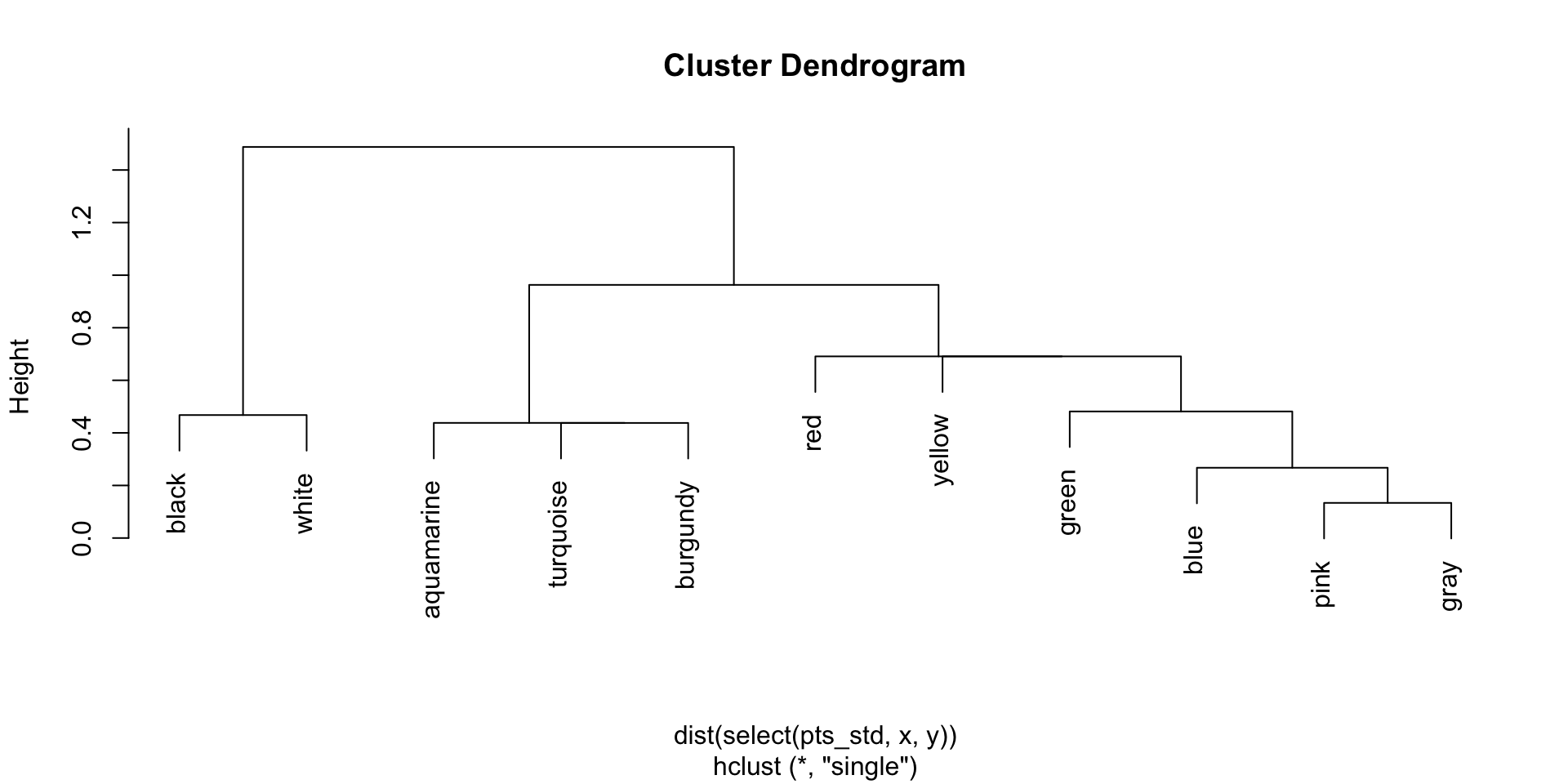
Complete linkage dendrogram

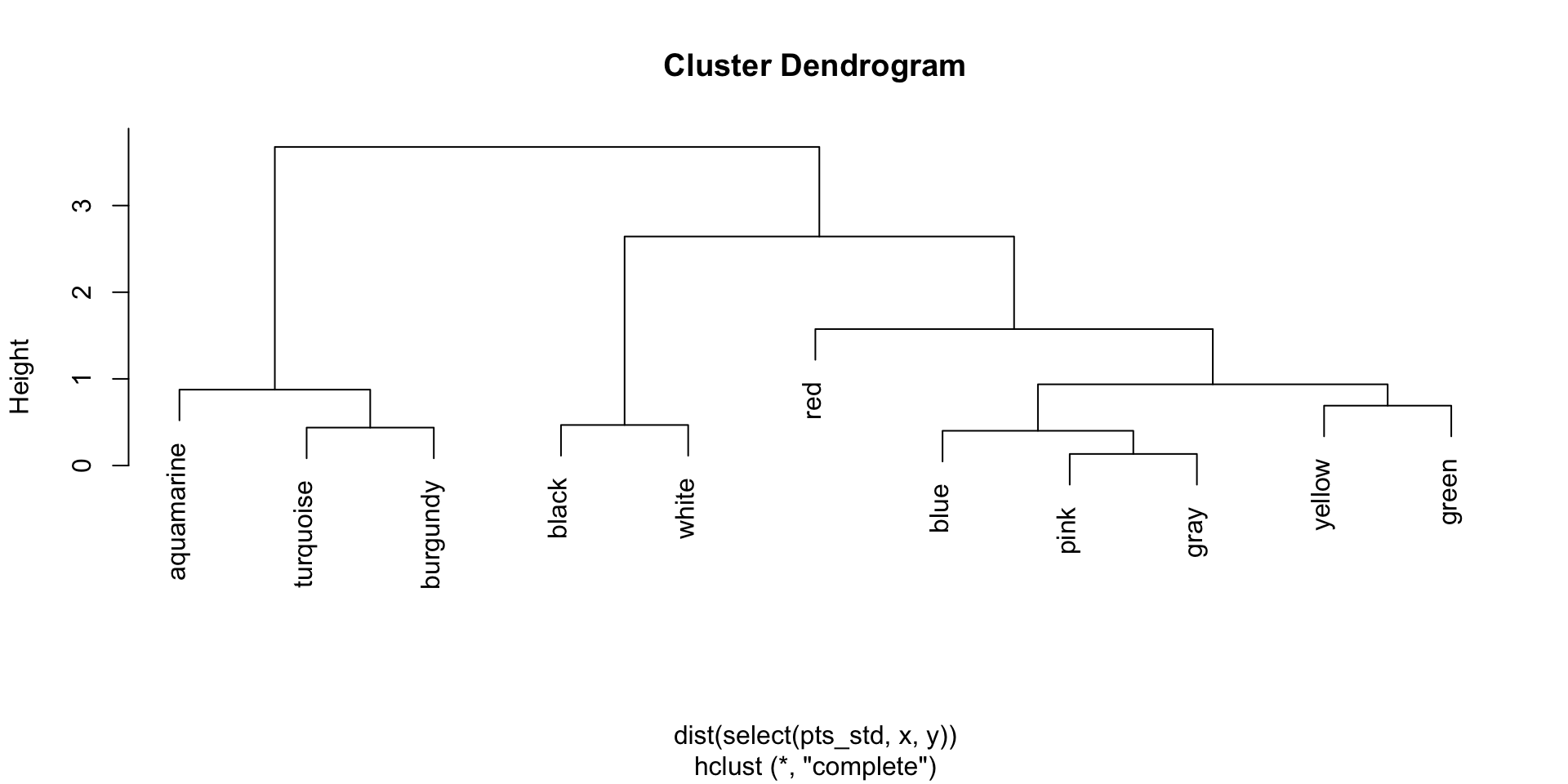
Average linkage dendrogram

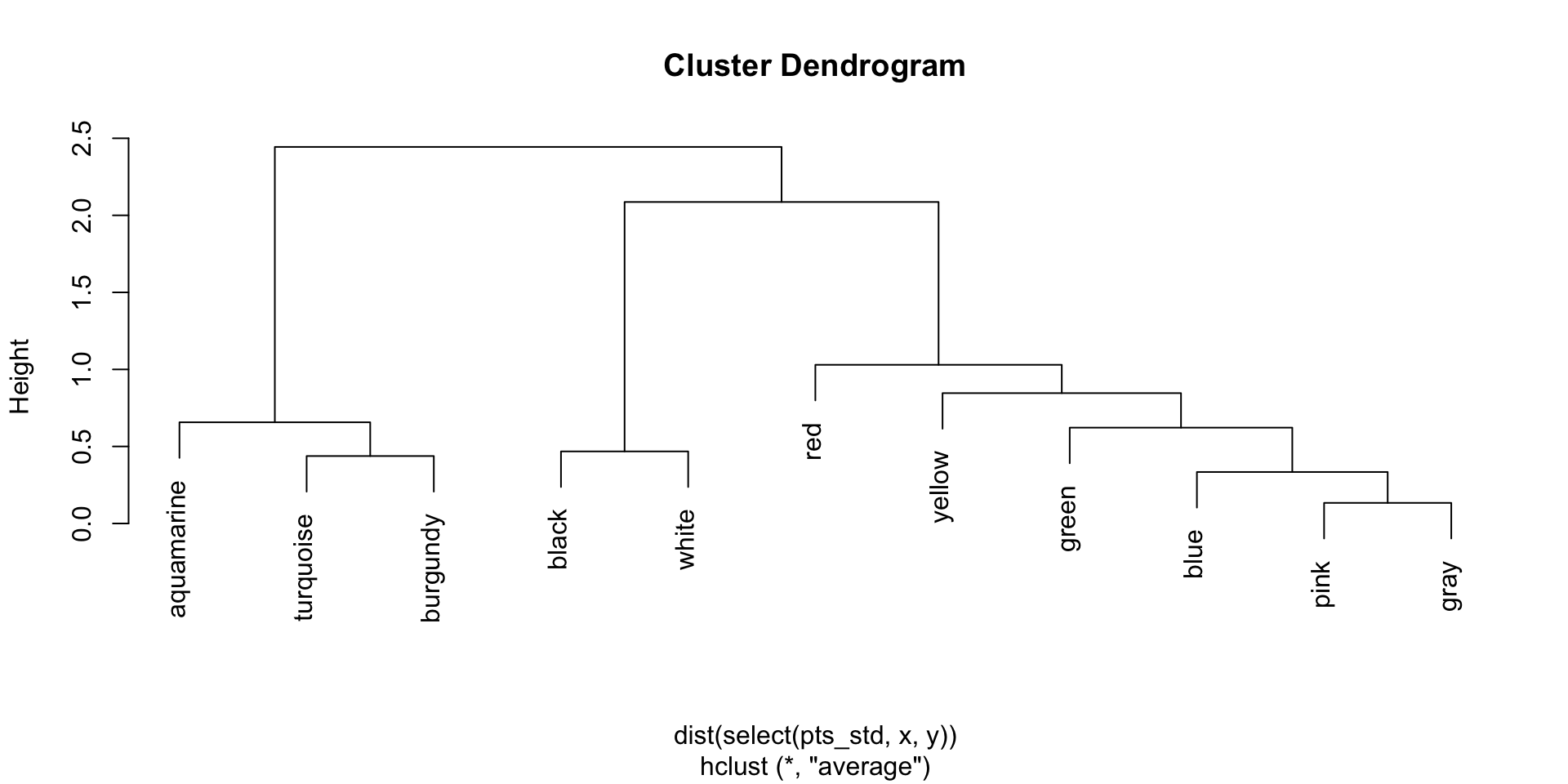
Ward’s linkage dendrogram

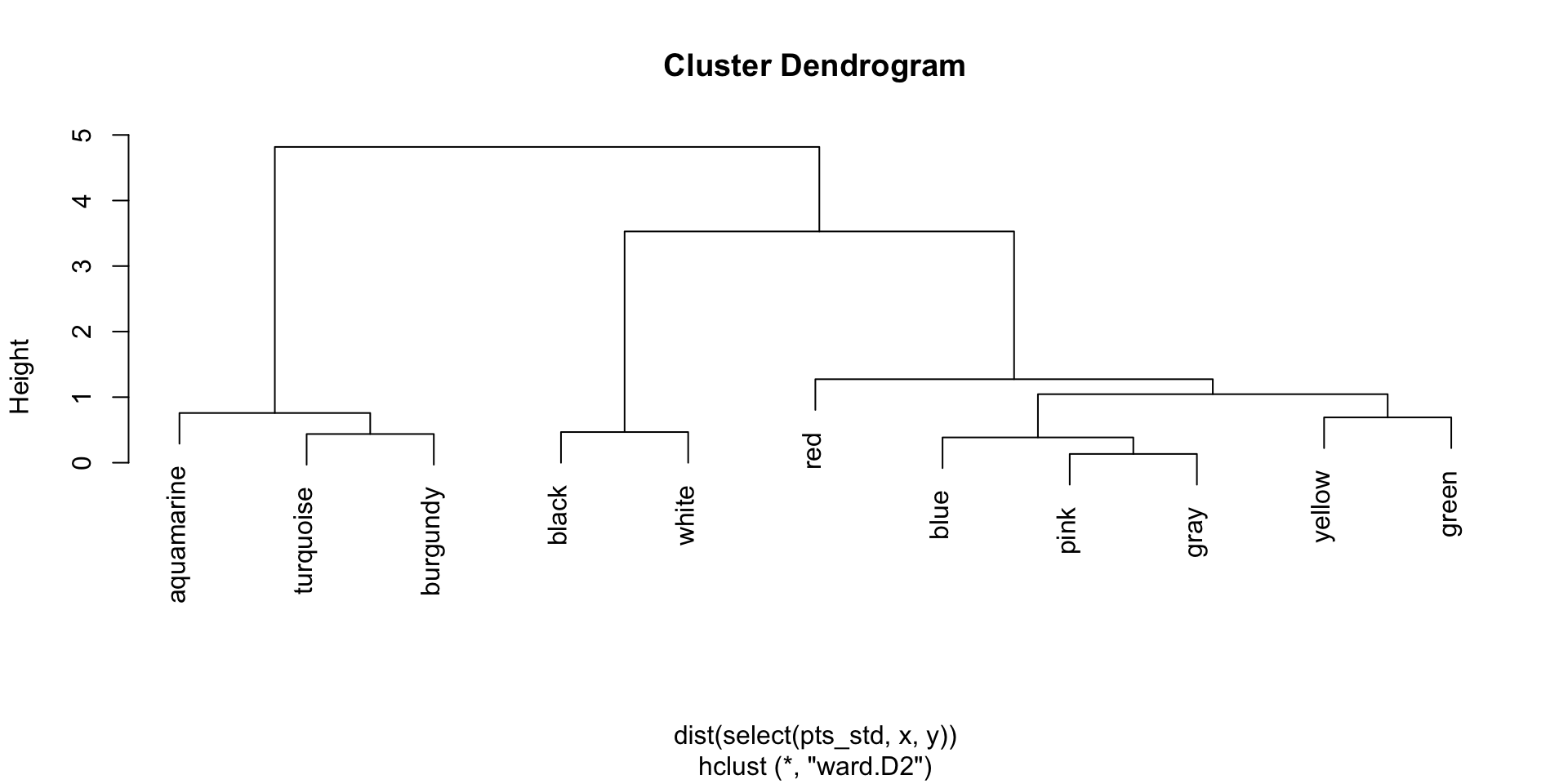
There is no single correct clustering

  • Clustering is an unsupervised method: we group observations with similar attributes
  • There is no response variable, so this is not a classification problem
  • Hence there is no “right” answer
  • The purpose of clustering is interpretation: finding similar observations so we can discuss them as a group

Measuring the amount of clustering

  • Let \(l(i)\) be the distance between word \(i\) and the first cluster/word it was merged with
    • If \(l(i)\) is small, it was similar to another word; if \(l(i)\) is large, it was only grouped later
  • Let \(l_\text{max} = \max_i l(i)\)

Then the agglomerative coefficient is: \[ \text{AC} = \frac{1}{n} \sum_{i=1}^n \frac{l_\text{max} - l(i)}{l_\text{max}} = \frac{1}{n} \sum_{i=1}^n \left(1 - \frac{l(i)}{l_\text{max}} \right) \]

  • \(\text{AC} \approx 0\): little cluster structure, words merged late
  • \(\text{AC} \approx 1\): lots of cluster structure, many words merged early

Reporting a clustering analysis

  • Cluster analysis is largely an exploratory visual method to show patterns in the data.
  • The parameters for cluster identification (data transformation, distance measure, cluster combination method) need to be reported.
  • The Methods section should describe the analytical procedure and the parameters used.
  • In the Results and Discussion, each tree plot (dendrogram) needs to be carefully discussed.

How many meaningful factors be observed in the plot?

K-means clustering

K-means clustering

  • \(K\)-means clustering works on a different principle: instead of hierarchically joining clusters, fix the number (\(K\)) in advance
  • Then choose clusters such that points within the cluster are similar to each other compared to points outside the cluster

That is, we find:

  • \(K\) cluster centers, \(\mu_1, \mu_2, \dots, \mu_K\)
  • Cluster assignments placing every observation in cluster \(1, 2, \dots, K\)

The objective

To find the cluster centers, we want to minimize the within-cluster variation. Let \(C_k\) be the set of observations in cluster \(k\): \[ W(C_k) = \sum_{i \in C_k} \|x_i - \mu_k\|_2^2 \]

The total within-cluster variation is \[ \sum_{k = 1}^K W(C_k) \]

We want to minimize this by choosing \(\mu_k\) and \(C_k\).

The optimization is hard

  • Actually optimizing the within-cluster variation is hard: there is a huge number of possible cluster assignments
  • (You can do the combinatorics)
  • Because cluster assignment is discrete, you can’t just take the derivative and set to zero to find the minimum
  • …and you can’t use gradient descent or any numerical optimizer
  • The actual optimization is NP-hard
  • But we can approximate it!

The usual K-means algorithm

  1. Choose \(K\)
  2. Select \(K\) distinct observations from the data and make these the initial cluster centers \(\mu_1, \dots, \mu_K\)
  3. Set the cluster assignments \(C_k\) to assign each observation to the nearest center (based on Euclidean distance)
  4. Update the cluster centers to be the mean of the observations assigned to that cluster
  5. Return to step 3

Eventually this will converge to a local optimum and you can stop

How do we choose K?

  • Again, this is an unsupervised problem, so there is no “correct” \(K\)
  • When data is 2D, you can eyeball the plot and judge the number of clusters
  • When data is 60D, you will find that difficult
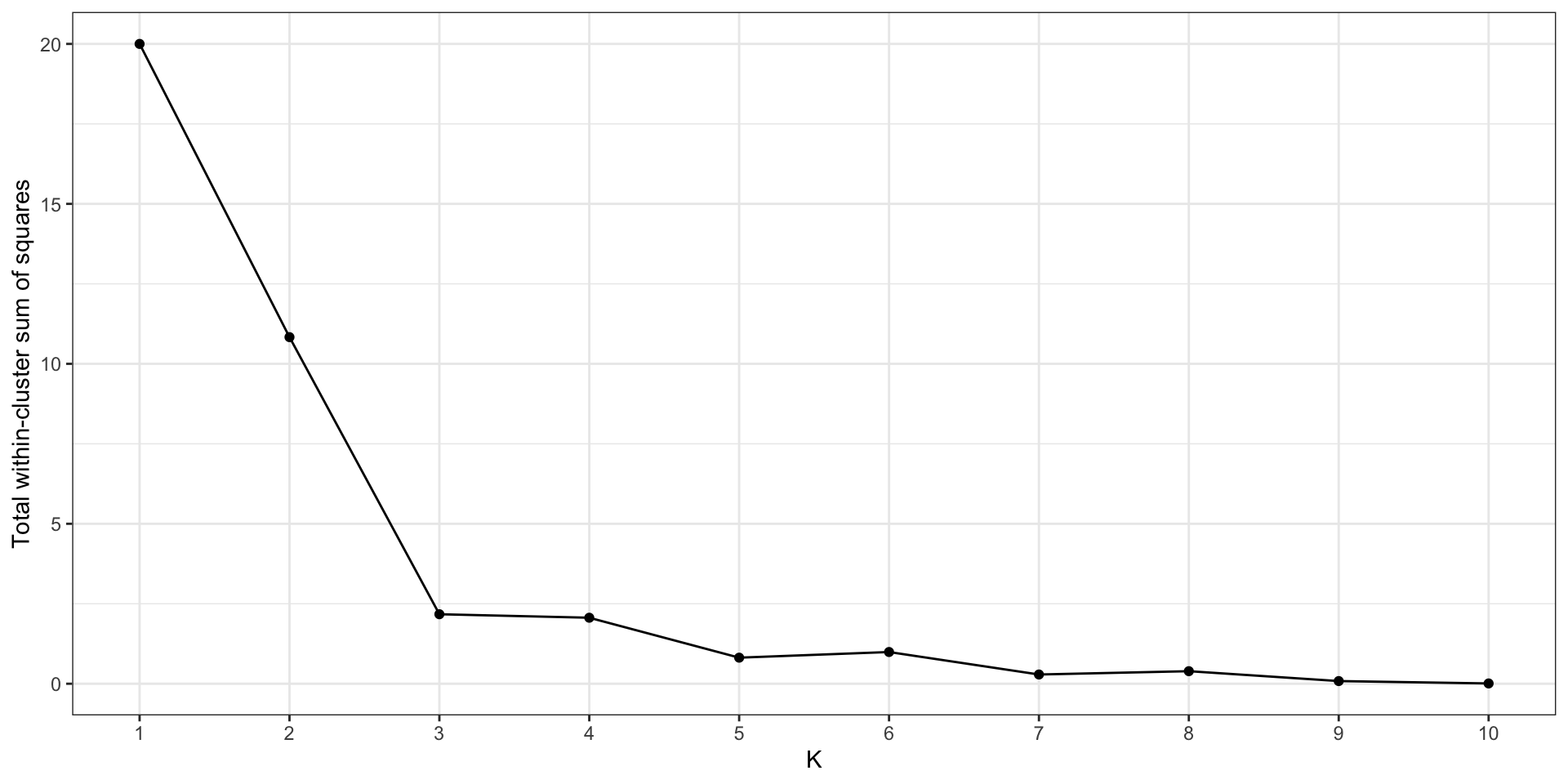
  • You can try to minimize within-cluster variation, but…
  • …the minimum is 0, when \(K = n\)

The elbow method

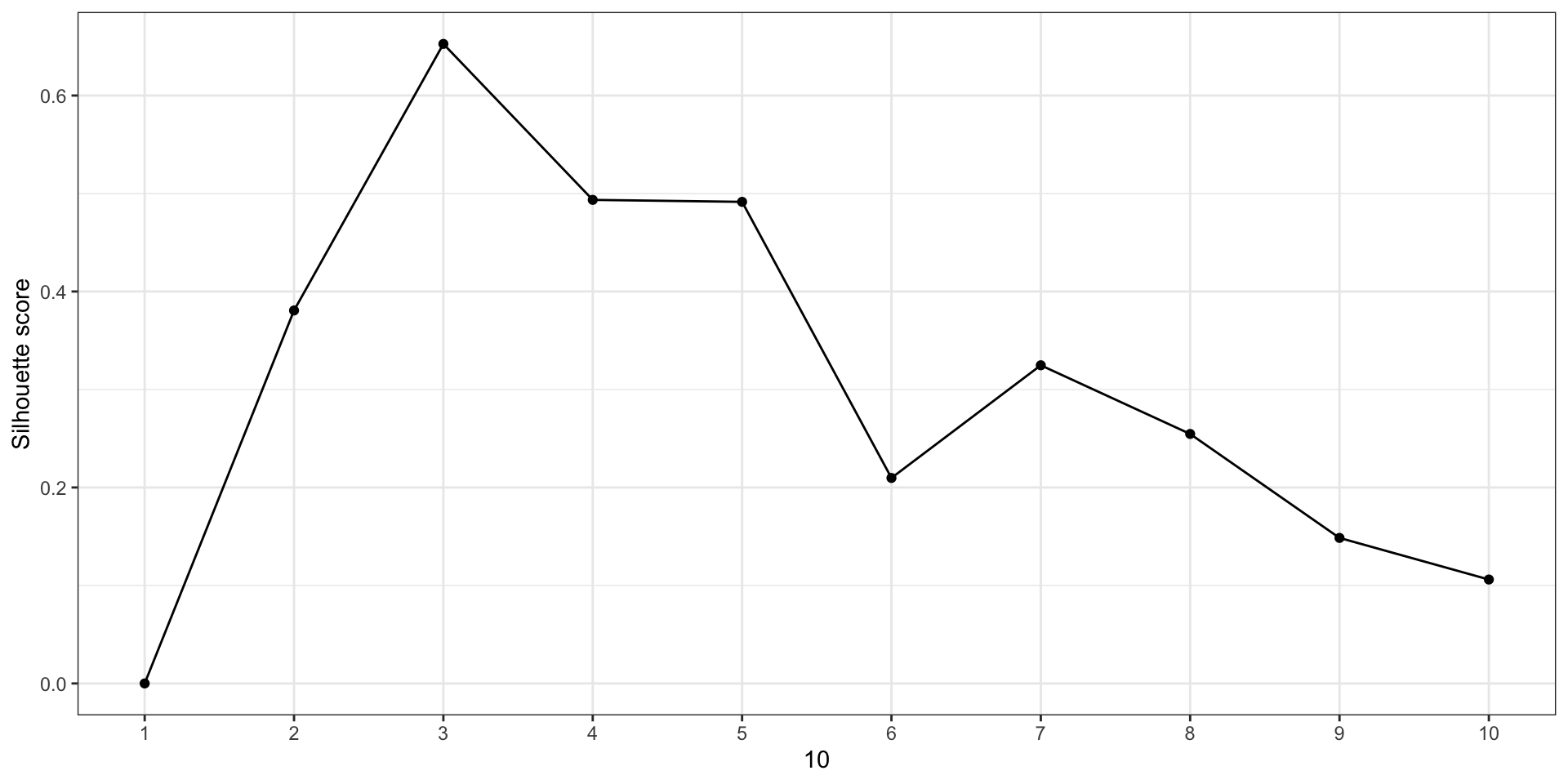
Silhouette method

  • For each observation \(i\), let
    • \(a(i) = {}\) mean distance between \(i\) and all other points in the same cluster
    • \(b(i) = {}\) mean distance between \(i\) and all points in the nearest other cluster

Then \[ s(i) = \frac{b(i) - a(i)}{\max\{ a(i), b(i) \}} \] (or 0 if no other points in the same cluster)

Average of \(s(i)\) is the silhouette score

Silhouette method